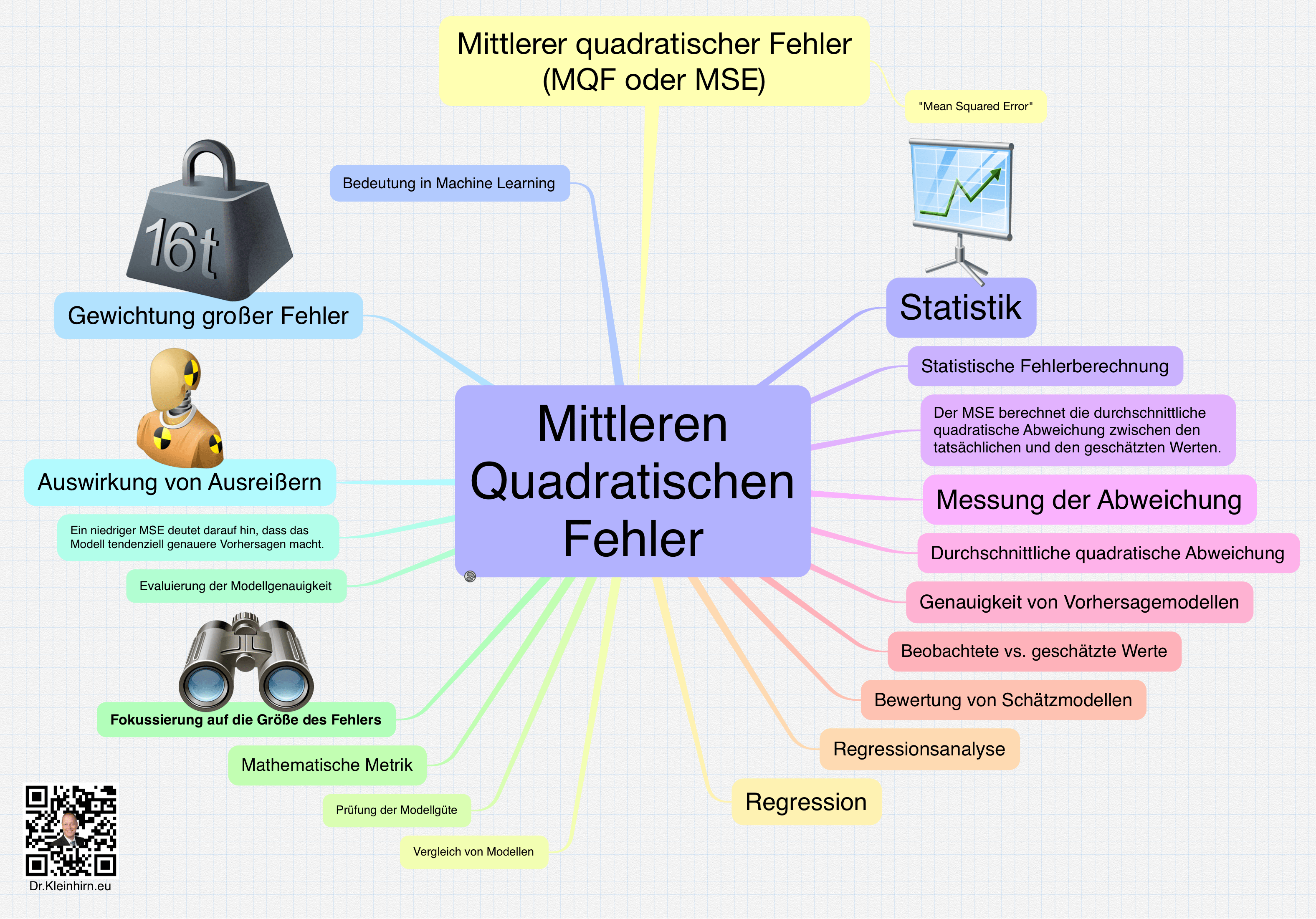
„Mittlerer Quadratischer Fehler“ oder auch „Mean Squared Error“ (MSE) genannt. Der Mittlere Quadratische Fehler ist eine Metrik, die verwendet wird, um die durchschnittliche quadratische Abweichung zwischen den geschätzten Werten und den tatsächlichen Werten in einem statistischen Modell zu messen. Es wird oft in Regressionsanalysen verwendet, um die Genauigkeit eines Schätzmodells zu bewerten.
Der MSE berechnet die durchschnittliche quadratische Abweichung zwischen den tatsächlichen und den geschätzten Werten. Ein niedriger MSE deutet darauf hin, dass das Modell tendenziell genauere Vorhersagen macht.
Wie könnte man das veranschaulichen:
„Stell dir vor, du versuchst, einen Ball in einen Korb zu werfen. Du wirfst den Ball mehrmals, aber du triffst nicht immer genau ins Zentrum des Korbes. Der Abstand zwischen dem Punkt, an dem der Ball landet, und dem Punkt, an dem du zielen möchtest, ist wie ein Fehler. Der Mittlere Quadratische Fehler ist wie der Durchschnitt dieser Fehler. Du schaust dir all die Male an, die du geworfen hast, und für jeden Wurf misst du den Abstand zwischen dem richtigen Punkt und dem, wo der Ball gelandet ist. Du nimmst all diese Abstände, quadrierst sie (machst sie also alle positiv, damit keine negativen dabei sind) und berechnest dann den Durchschnitt davon. Wenn der Mittlere Quadratische Fehler klein ist, bedeutet das, dass du den Ball im Durchschnitt ziemlich nah am Korb geworfen hast. Wenn er groß ist, dann warst du vielleicht nicht so genau. Das hilft uns, zu verstehen, wie gut wir beim Werfen in den Korb sind.“
Es ist eine wichtige Metrik, um die Leistung von Regressionsmodellen zu bewerten, aber es ist wichtig zu beachten, dass der MSE sehr empfindlich gegenüber Ausreißern ist, da die quadrierte Abweichung in die Berechnung eingeht. In einigen Fällen kann es sinnvoll sein, alternative Metriken zu verwenden, wenn Ausreißer ein Problem darstellen.
Download mittleren-quadratischen-fehler.pdf.